AI Models

When it comes to Artificial Intelligence (AI), the most iconic model structure is the neural network.
We introduce this concept here in a way that directly builds upon the modeling principles you've studied so far — especially those involving inputs, outputs, parameters, and optimization.

At its core, a neural network is a sequence of mathematical operations that transforms inputs into outputs, with the aim of reproducing or predicting observed data.
The simplest unit within a neural network is the neuron.

A foundational type of neuron, called a perceptron, operates with two key parameters:

a weight (w) that scales (multiplies) the input
a bias (b) that shifts (adds to) the result

This structure is mathematically equivalent to a linear model, where the relationship between input and output is defined by a straight line.
So, even a single perceptron can be seen as a basic linear regression model.

Let's examine a simple case:
Consider a neural network with just two neurons, acting on two input variables, $x_1$ and $x_2$ .
Each neuron has its own weight and bias, giving a total of four parameters.

The output $y$ of this mini-network is computed as:

y = x_1 \cdot w_1 + b_1 + x_2 \cdot w_2 + b_2

This expression combines both input contributions linearly:

x Input

y Output

As in all modeling frameworks, the objective is to optimize the parameters (w₁, w₂, b₁, b₂) so that the output of the model matches the experimental data as closely as possible.
In AI, this optimization process is commonly referred to as training the model.

Once training is complete and the best parameter values have been identified, the model is used to generate predictions in a process called validation.
During validation, no further parameter updates are allowed — it's the test of how well the trained model performs on unseen data.

Now it's your turn!
Try to manually “train” this simple neural network by adjusting the four parameters to match the desired output.

The Loss (MSE) — Mean Squared Error — will tell you how close you are.
A lower loss means a better fit.

Simple Neural Network Trainer

Challenge:

Input X1: 0.50

Input X2: 0.80

Target Output: 0.00

Weight w1: 0.00

Bias b1: 0.00

Weight w2: 0.00

Bias b2: 0.00

Predicted Output: 0.00

Loss (MSE): 0.0000

Remember: the underlying function stays constant every time you run the exercise.
That means the optimal values for the weights and biases are fixed — can you find them?

📝Note

You might quickly realize how difficult it is to manually train even such a small neural network.
As the number of neurons (and thus parameters) increases, the difficulty grows exponentially.
This is why AI training requires powerful optimization algorithms and significant computational resources to efficiently search for the best parameter combination.

The Curse of Dimensionality

In the world of Artificial Intelligence, especially in deep learning, neural networks with many layers — called deep neural networks — are extremely common.
Each of these layers is made up of neurons, which can come in many different forms and configurations, giving the network a variety of capabilities and attributes.

As you've seen before, each neuron contributes parameters — typically weights and biases — to the model.
As the number of neurons increases, so does the total number of parameters. This leads to a phenomenon known as the curse of dimensionality.

Let's take a look at a simple example.
Even a relatively basic neural network with just 22 neurons can have over 100 parameters:

Now consider large-scale models used in natural language processing (like ChatGPT).
These models are massive — and their number of parameters is staggering:

GPT-3.5 has approximately 175 billion parameters
GPT-4 Turbo pushes this to 1.8 trillion parameters!

⚠️What's the problem with more parameters?

While more parameters give a model greater flexibility and learning capacity, they also come with major challenges:

Overfitting: With too many parameters, the model can "memorize" the training data instead of learning general patterns (already discussed in Module-2).
Increased computational cost: More parameters require more memory and longer training times.
Data requirements: The higher the number of parameters, the more data is needed to properly train the model.
Interpretability: As models grow more complex, understanding how they make decisions becomes increasingly difficult.

This exponential growth in model complexity with added dimensions is what we call the curse of dimensionality.
It's one of the central challenges when working with AI models — especially when trying to apply them in fields like sport science, where data may be limited or noisy.

Understanding this concept is crucial when choosing or designing models for physiological performance prediction, injury prevention, or workload optimization.

How does an LLM work?

Throughout this course, we've conceptualized models as services that take inputs (x) and produce outputs (y) by adjusting parameters to find the best fit. Large Language Models (LLMs) like ChatGPT work on exactly the same principle—but at an enormous scale.

Think of an LLM as a text prediction service. Just like our VO₂ model takes power input and predicts oxygen consumption, an LLM takes text input and predicts the next word that should come after it.

The Input (x): Instead of power measurements or heart rate data, the input is text—words converted into numbers that the model can process. Each word becomes a position in a high-dimensional mathematical space.

The Output (y): Rather than predicting VO₂ or lactate levels, the model predicts probabilities for each possible next word. "The weather is..." might have high probability for "sunny" or "cloudy," low probability for "bicycle."

The Parameters: Remember how our HR_max model had 2 parameters, and our chicken growth example had up to 5? An LLM like GPT-4 has 1.8 trillion parameters—all weights and biases like the neural network you manually trained earlier, but scaled up massively.

The Training Process: Just like we optimized RMSE in Module 2, LLMs are trained by showing them billions of text examples and adjusting those trillion parameters until the model gets better at predicting the next word. This is the same parameter estimation process we've used throughout—just with astronomical amounts of data.

Why it seems "intelligent": The model isn't actually understanding language the way humans do. Instead, through processing vast amounts of text, those trillion parameters have learned incredibly sophisticated statistical patterns about how words typically follow each other. It's pattern recognition at an unprecedented scale.

When you ask ChatGPT "What's the best training method for VO₂max improvement?", it's not consulting a physiology textbook. Instead, it's using its parameters to predict, word by word, what text would most likely follow your question based on the patterns it learned during training.

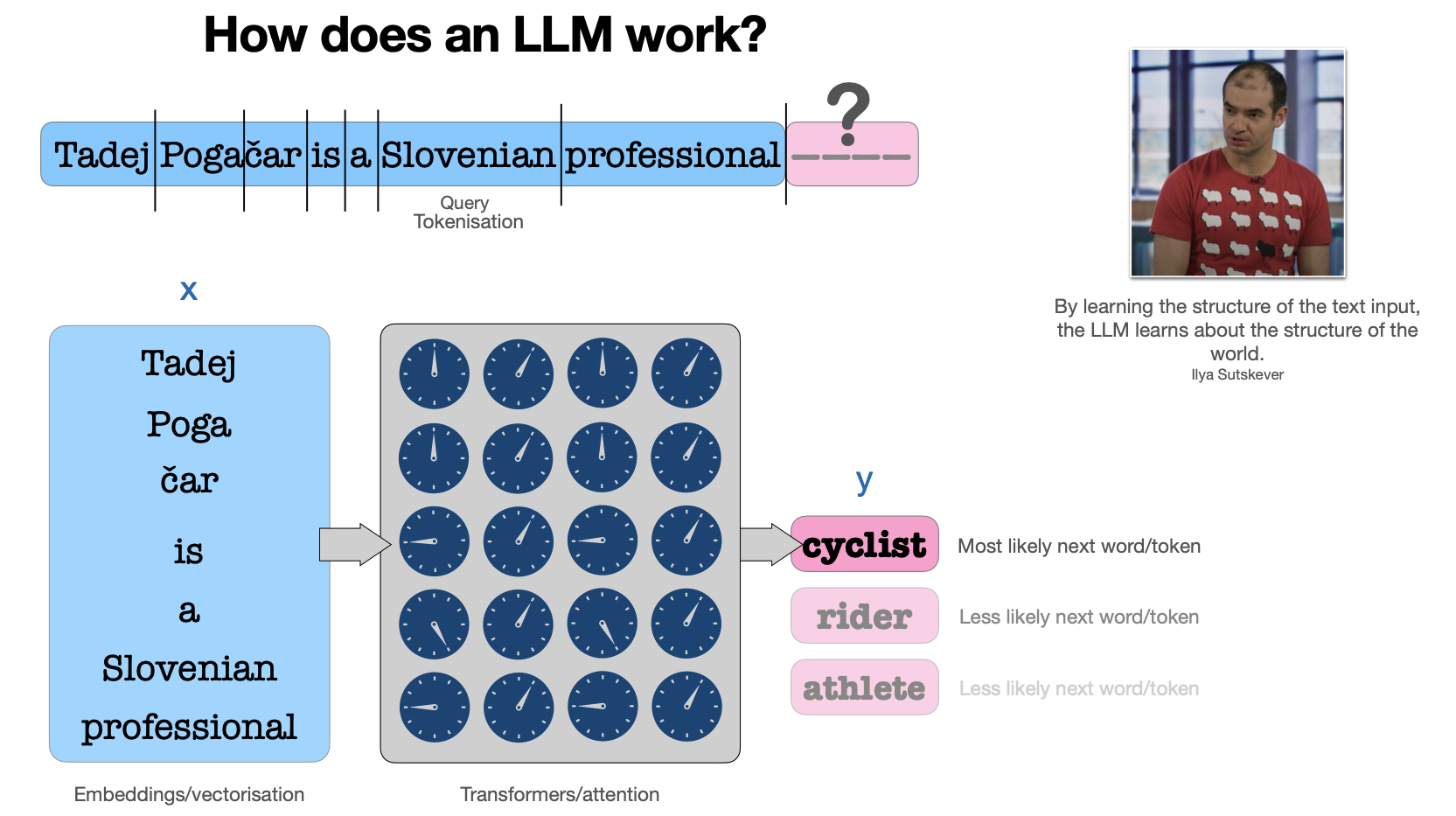
This is fundamentally the same modeling approach we've used for heart rate prediction, lactate clearance, and power-duration curves—just scaled up to handle the incredible complexity of human language. The core principle remains: input → parameters → output, with optimization driving the learning process.

Checkout

Well done, you were able to complete the fifth module of this course.

👮🏻‍♂️Checkpoint

At the end of Module-5 you should be able to reply to these questions with confidence:

What are the fundamental components of a perceptron (weights and biases), and how does a simple neural network relate to linear regression models?
What is the difference between the training phase (parameter optimization) and validation phase (performance testing) in neural network development?
How does the curse of dimensionality manifest as neural networks grow larger, and why do models like GPT-4 require massive computational resources?
How do the challenges of overfitting, data requirements, and interpretability increase with the number of parameters in AI models applied to sports science?